TESTING REGRESSION ESTIMATES
INTERMEDIATE VARIABLES IN CB SEM MODEL (PART 1)

At the end of the SEM model analysis step, we are basically done. However, we need to know whether the estimates (regression weights) extracted from the above SEM model analysis step are reliable or not. then you need to take this additional step of testing Bootstrap. It can be said that this is the step to evaluate the reliability of the estimates from the SEM model.
The first step, in the SEM screen, go to View/Analysis Properties/Bootstrap. Check the Perform bootstrap box and enter the bootstrap sample number. Normally, choose the number of bootstrap samples to be about 1000 (according to Preacher, K. J., and Hayes, A. F., 2008), moreover it is OK, but the machine is a bit heavy, 1000 is enough for the test to converge, larger is also fine. but it’s not really necessary. Now the program will generate 1000 samples, then analyze the SEM for these 1000 samples, and return the mean of the estimates in each bootstrap model.
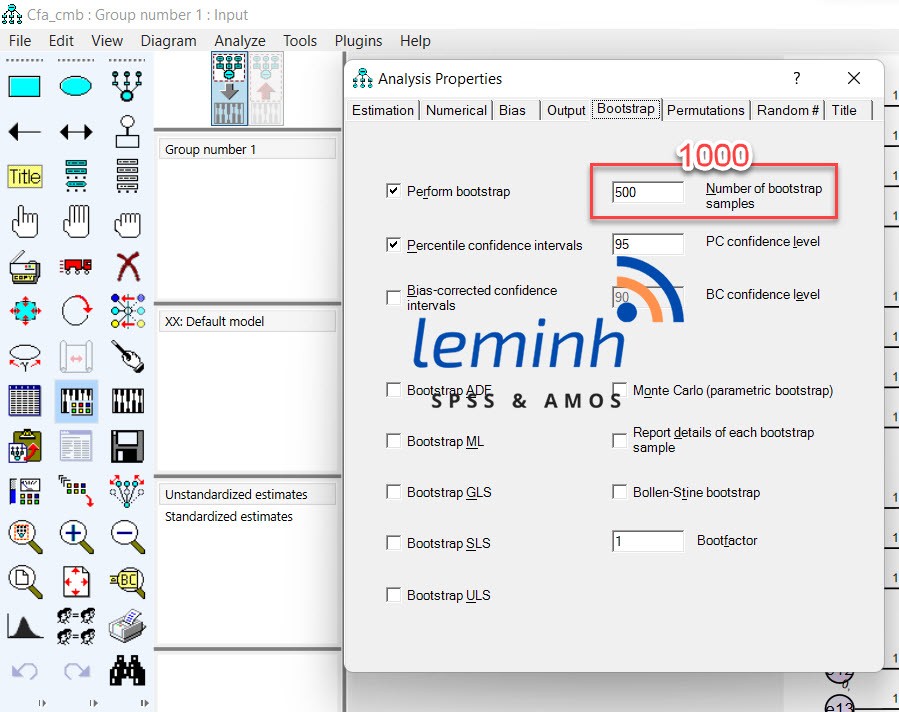
Select Viewtext to display the Amos Output dialog box. Click to select Standardized Regression Weights (1) and select Bootstrap standard errors (2). Right click and select copy to paste into excel (3).
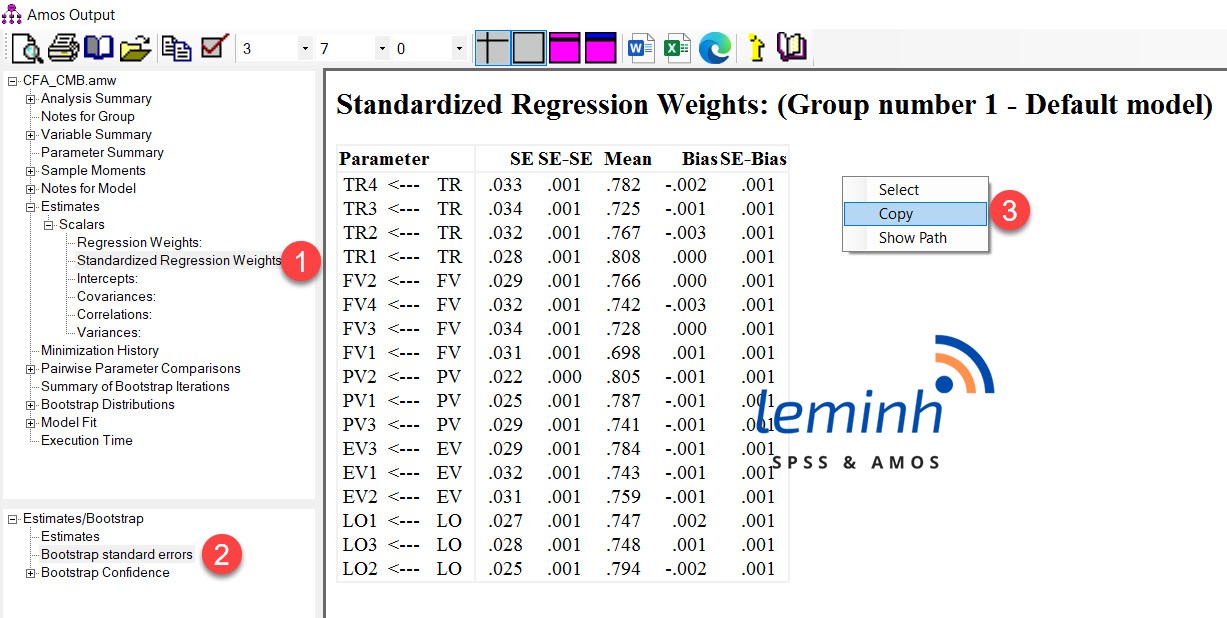
We calculate the CR index according to the formula shown in the figure below. CR < 1.96, it can be concluded that the bootstrap test is satisfactory.
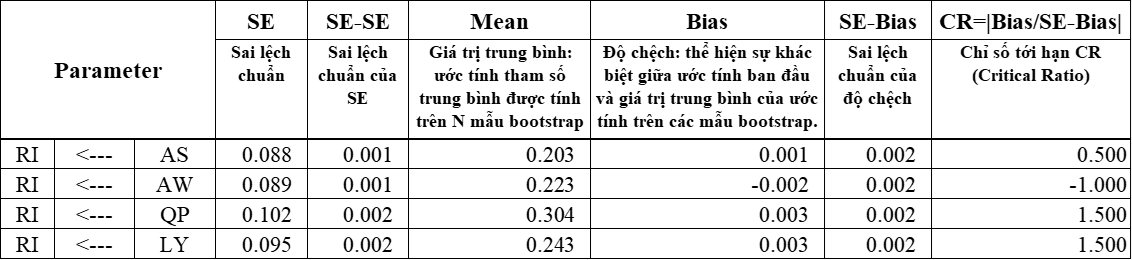
|CR| values < 1.96, so it is concluded that the bias between 2 samples (n – collected samples) and sample (N – repeated samples according to bootstrap) is not statistically different from 0. In other words, there is no difference between sample (n) and (N). Therefore, it is concluded that, sample (n) is reliable, the estimates in the SEM model are reliable.
ABS(CR) value < 1.96 as suggested by Gao et al (2008). In 2013, Byrne published the second edition of the book Structural equation modeling with AMOS: Basic concepts, applications, and programming, he proposed the ABS(CR) index ≤ 2; However, in the third edition in 2016, Byrne revised the ABS(CB) index to < 1.96.
Basically, when testing the reliability of estimates through the Bias CR critical index, in many cases it is difficult to achieve for many different reasons. So usually, I often conclude through the criterion of small bias (≤ 5‰). And I rarely see any international articles mentioning Bias’s CR index. However, they refer to Bootstrap bias-corrected confidence intervals at the 10% (or 5%) level of significance to evaluate mediating relationships in SEM (i.e., testing whether a mediating variable in the research model Whether the research really plays the role of an intermediary variable or not, this has important implications in understanding and providing solutions for each specific problem).
Next, we will learn how to evaluate intermediate variables in SEM.
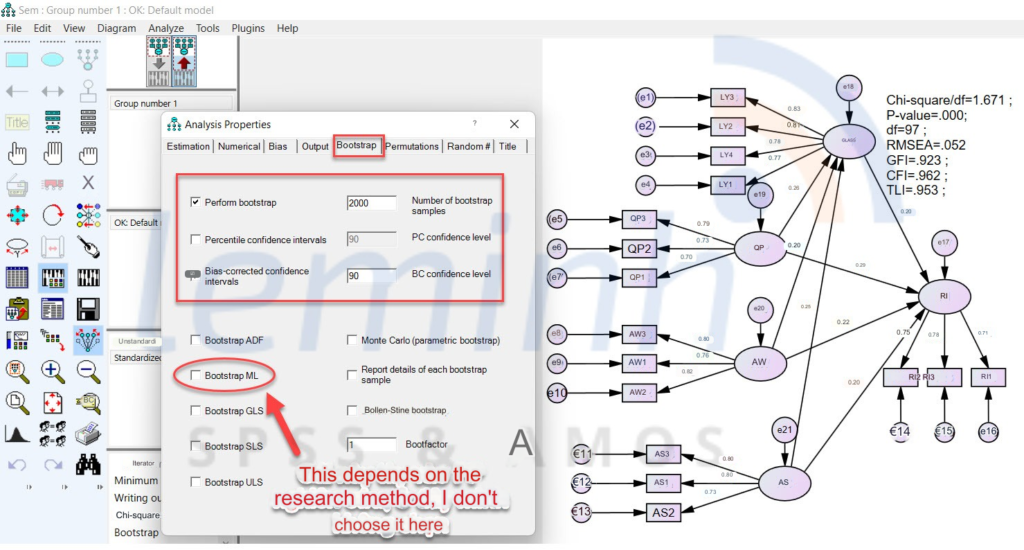
First, we declare in the bootstrap section as follows:
Then, we need to define the total indirect effect value variables in the model. The first step is that we label the regression weight of each relationship to consider as shown.
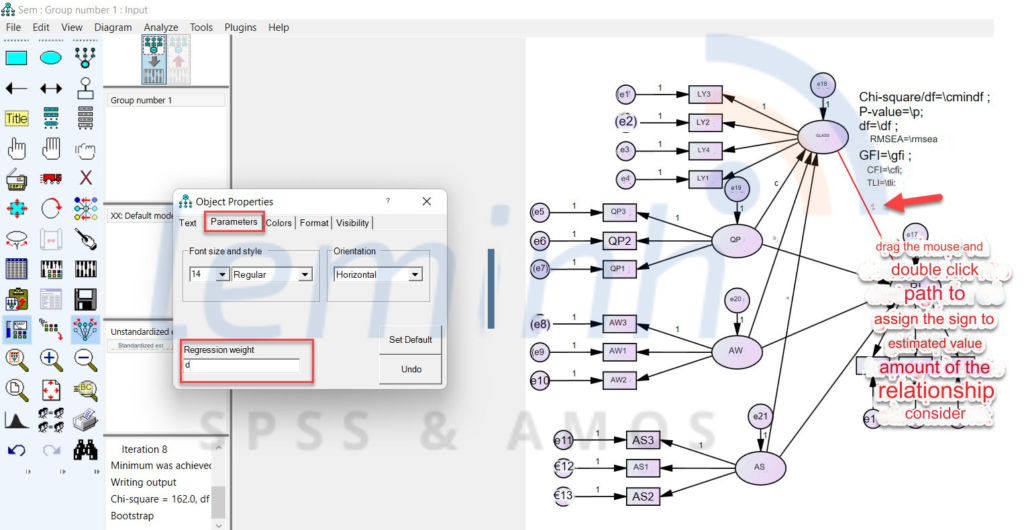
Step two, left click on the words Not estimating any user-defined estimand and click Define new estimands. And write code similar to the image below. To determine the formula for calculating the value of indirect effects in the model, we further study Kline (2016).
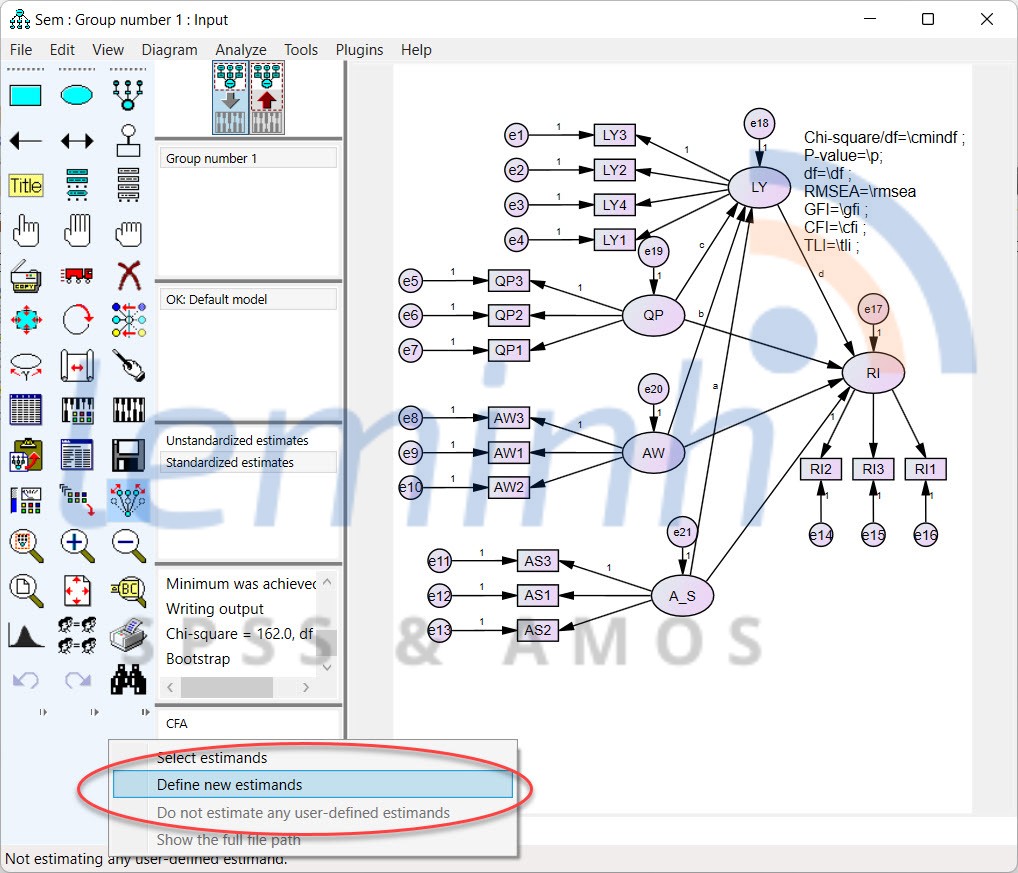
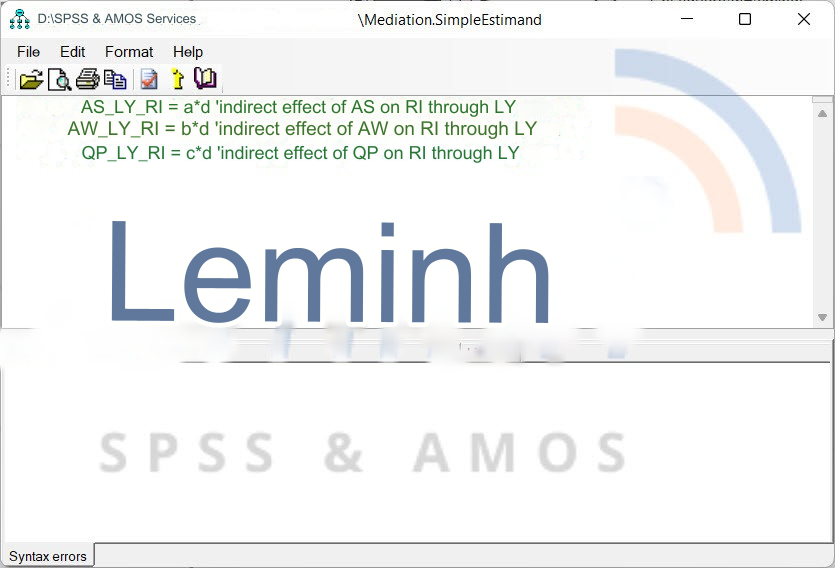
After finishing writing, we save it with any name and close it. In case the code structure is incorrect, the program will report an error in the Syntax errors section, and we will fix it according to their instructions. Next, we run the analysis, and read the results in Output SEM. There is one thing we need to note, with the estimated code file defined after each analysis run, AMOS will not load itself, but will return the default form, and therefore the user needs to reload it the next time it runs.
In case of structural errors, the program will display a notification. At this point, you need to right-click on the text Not estimated any user-defined estimate and click Edit mediation to edit.
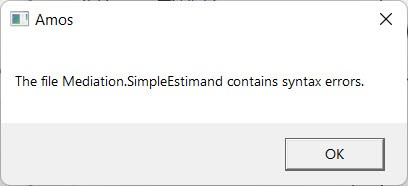
Our syntax is normal, but the variable name AS in SEM is not accepted, so we need to change the name to A_S. Read the results.
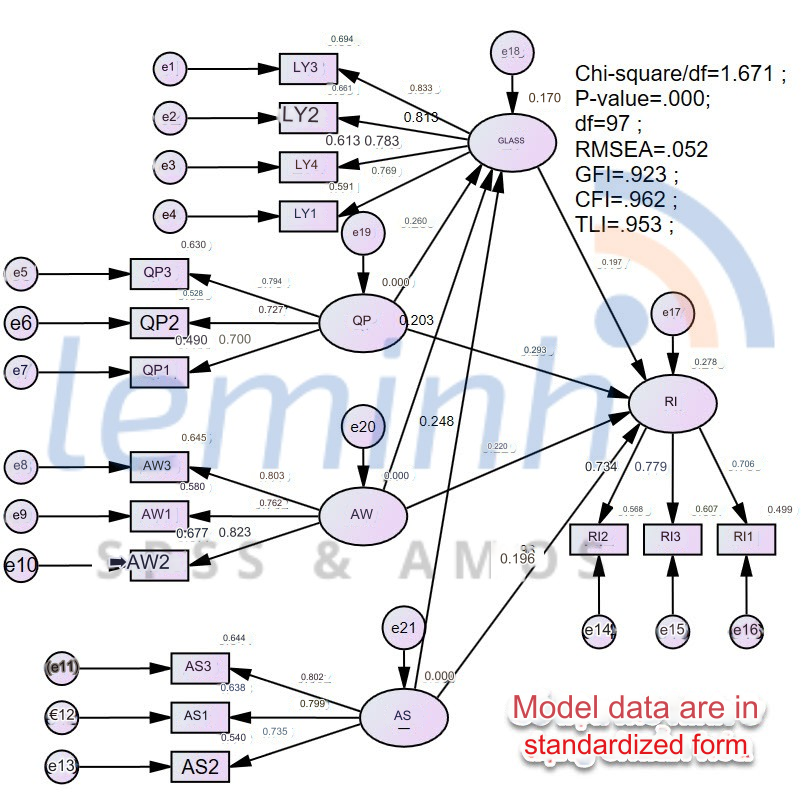
User-defined mediation estimates appear when we select User-defined estimands.
I usually present the results in the form of a table as follows. People often ask, so it’s convenient to write them down here. Note that in research published in Vietnam, we should Vietnameseize the words.

A bootstrap p value ≤ 5% means that the sum of the indirect effects is significantly different from zero at any level of significance. In other words, there exists an intermediate relationship of the LY variable in the research model.
One thing to note is that the estimated values obtained from coding are unstandardized values, but this is not too important because we only need to conclude whether or not an intermediate relationship exists in the model. study. To evaluate the influence of independent variables, including direct and indirect effects, we need to consider the Matrices section (to appear, in the SEM Output declaration section before running we remember to choose
 .
.
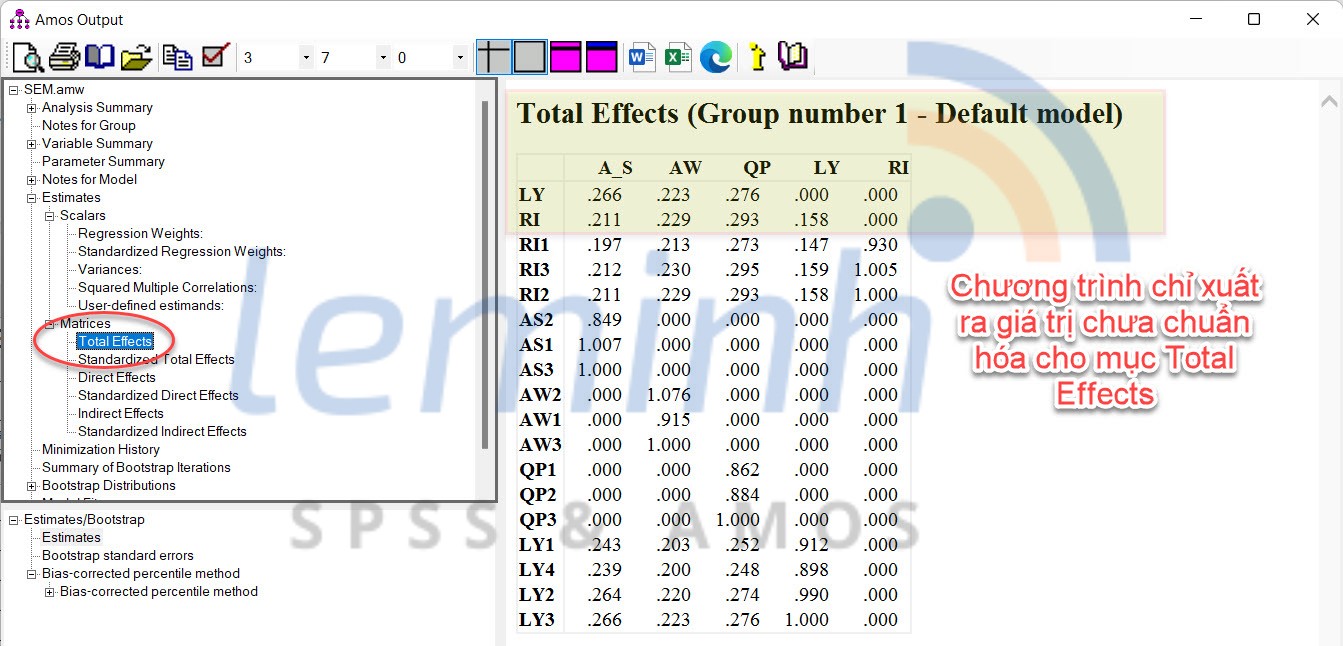
We need to note that the values in the Total Effects table are not standardized by the program. To calculate the sum of standardized estimates, we need to perform manual calculations according to the formula of Kline (2016). Specifically, in this article we can calculate as follows.
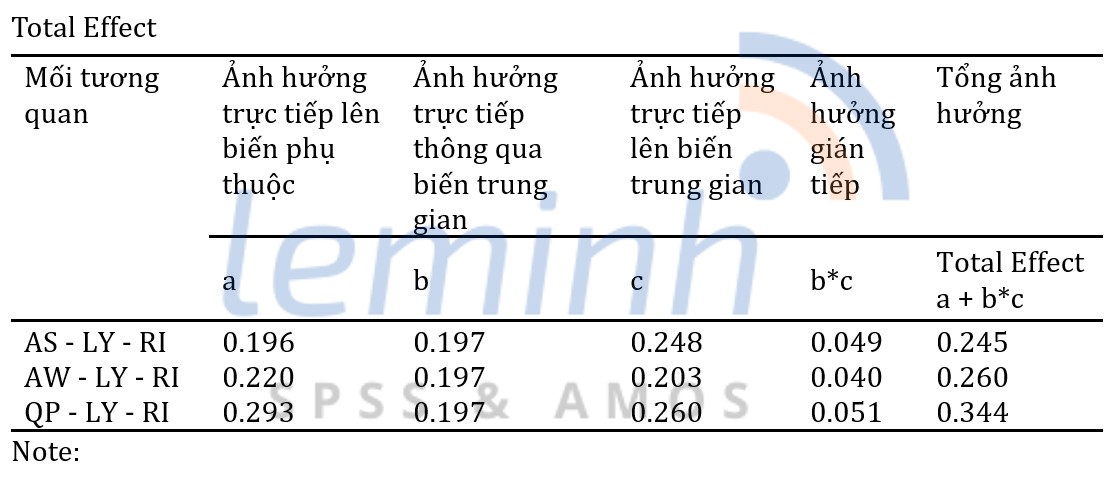
T-statistics index
Next we will calculate the t-statistics. To calculate t-statistics we need the beta coefficient and standard error. To get the beta coefficient we go to Estimates -> User-defined estimands and from Estimates/Bootstrap we select Bias-corrected percentile method. To get the standard error (SE) we go to Estimates -> User-defined estimands and from Estimates/Bootstrap we select Bootstrap standard errors. Divide the beta coefficient by the standard error to get the t-statistics value (Collier, J. E., 2020).
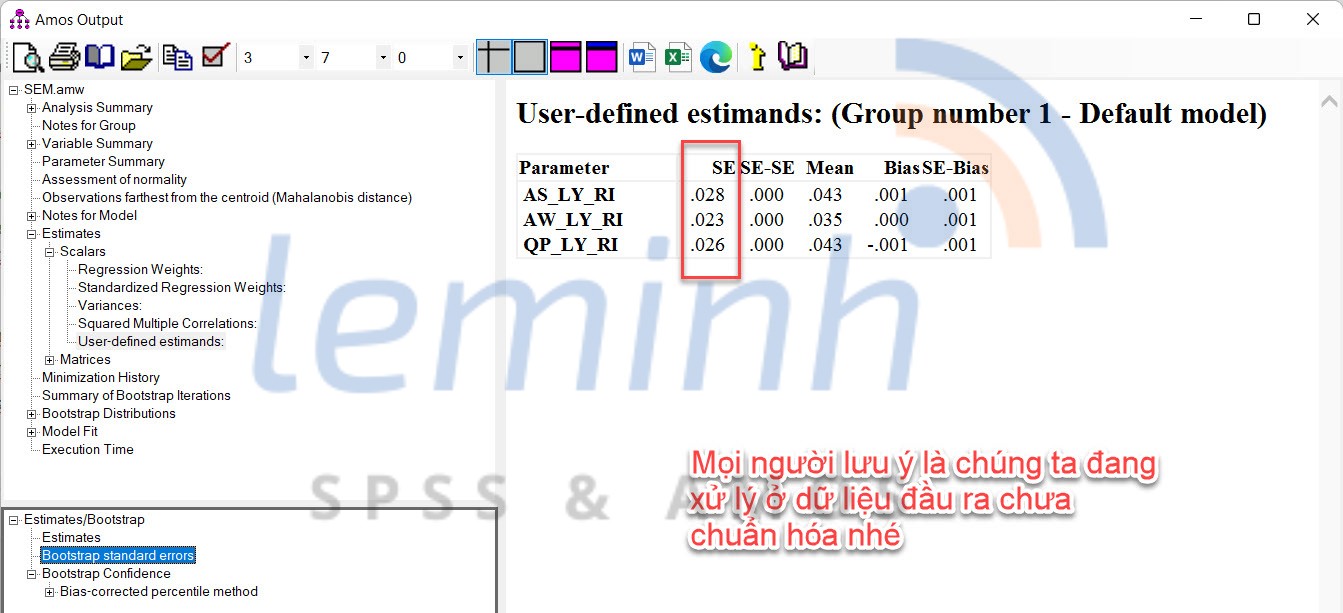
With AS-LY-RI: t-statistics is 0.042/0.028 = 1.500; AW-LY-RI: t-statistics is 0.035/0.023 = 1.522; QP-LY-RI: t-statistics is 0.044/0.026 = 1.692.
The results of mediation analysis will be presented in the following table.
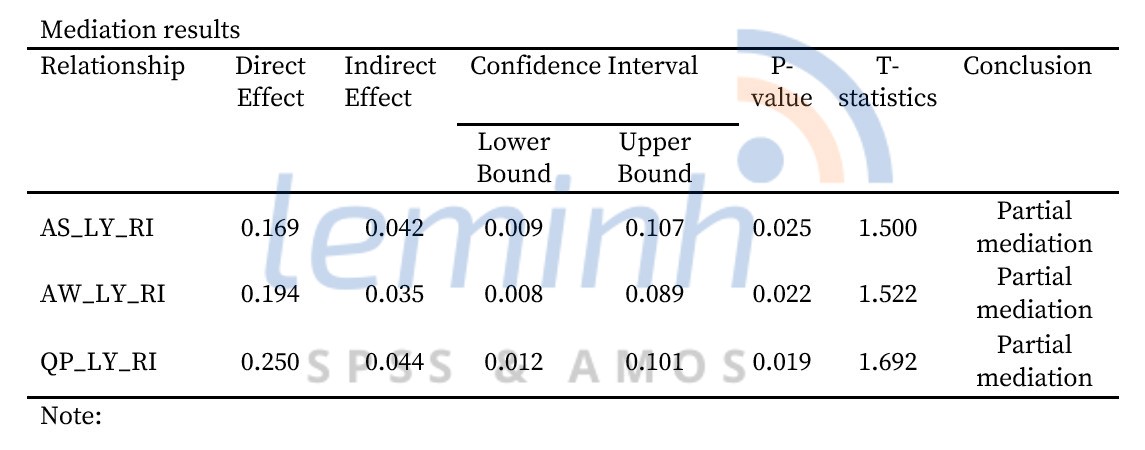
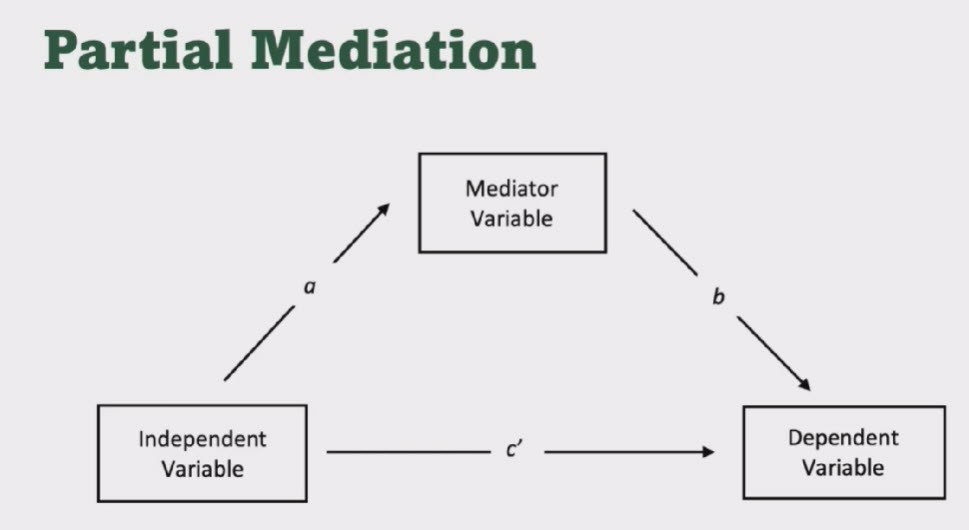
Need to say a little more in the conclusion, when the direct effect is or is not statistically significant (don’t care) and the indirect effect is not statistically significant, we conclude that there is No mediation. When the direct effect is statistically significant and the indirect effect is statistically significant, we conclude Partial mediation. And when the direct effect is not statistically significant and the indirect effect is statistically significant, we conclude Full mediation.
| Indirect relationship | Direct relationship | Conclude |
| a*b is statistically significant (i.e. both a and b are statistically significant) | c’ is statistically significant | Partial mediation |
| a*b is statistically significant (i.e. both a and b are statistically significant) | c’ is not statistically significant | Full mediation |
| a*b is not statistically significant (i.e. either a or b is not statistically significant) | Don’t care about c’ | No mediation |
To evaluate the level of strong/medium/weak influence (mediating effect sizes), we refer to documents by Cohen (1988; 2013): beta from ±0.1 to ±0.3 is small; A beta of ±0.3 to ±0.5 is average; and a beta of ±0.5 or more is strong. The beta value (estimate) is within ±1.
At this point, we have completed the mediation analysis for the SEM model. A small suggestion is that we should not over-complicate the problem in mediation analysis, the problem lies in the solutions and results achieved to meet the requirements for the research objectives.
References:
Amos Development Corporation, 2010. User-defined estimates. http:// amosdevelopment.com /features/ userdefined/ userdefinedsimple/ Tutorial2/ pdf/ SimpleUserDefined2 .pdf. (Accessed May 10, 2021).
Byrne, B. M. (2013). Structural equation modeling with AMOS: Basic concepts, applications, and programming. Routledge.
Byrne, B. M. (2016). Structural equation modeling with AMOS: Basic concepts, applications, and programming. Routledge.
Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Academic press.
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2013). Applied multiple regression/correlation analysis for the behavioral sciences. Routledge.
Collier, J. E. (2020). Applied structural equation modeling using AMOS: Basic to advanced techniques. Routledge.
Gao, S., Mokhtarian, P. L., & Johnston, R. A. (2008). Nonnormality of data in structural equation models. Transportation Research Record, 2082(1), 116-124.
Kline, R. B. (2016). Principles and practice of structural equation modeling. Guilford publications.
Preacher, K. J., & Hayes, A. F. (2008). “Assessing mediation in communication research”. London: The Sage sourcebook of advanced data analysis methods for communication research.






