HIGH-LEVEL STRUCTURE MODEL
The main reason given by Hair and colleagues (2013) to explain why it is necessary to use a second-order structure in SEM models is because it helps research reduce the number of relationships in the model, and thereby making the analysis of SEM models easier.
In addition, when factors in the research model are highly correlated, the structural model will be biased due to multicollinearity. So to eliminate multicollinearity, one of the effective ways is to use a high-order structural model.
When we use secondary structure in research, the most important thing to pay attention to is the purpose of the research model.
In a PLS SEM model using SmartPLS, all latent variables must have at least one observed variable. Therefore, Lohmöller (1989) and Wold (1982) introduced an approach called recurring indicators. There, the observations of the first-order variable will be included in the second-order variable. For example, picture below:
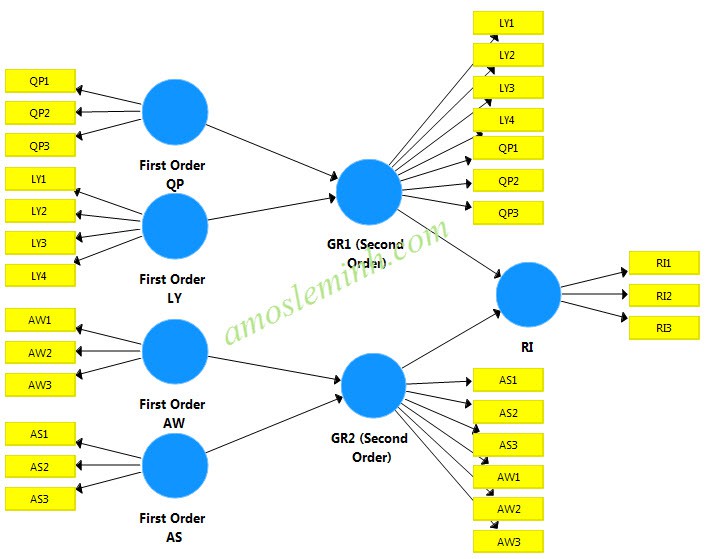
At this point, our model only has two basic hypotheses: GR1 –> RI and GR2 –> RI. Thus, it can be seen from the model that there are four research hypotheses. After using quadratic variables, the model is reduced to two research hypotheses. This helps the study reduce analytical complexity. However, it needs to be added that when using a quadratic variable model, the author’s research theory must support this.
In the CB SEM model, AMOS software is used to simulate SEM containing a secondary structure that is different from SmartPLS. In AMOS, quadratic (second order) variables contain no observed variables (items), but for the model to be deterministic, you need to set constraint coefficients on at least one path for each second-order variable. For example:
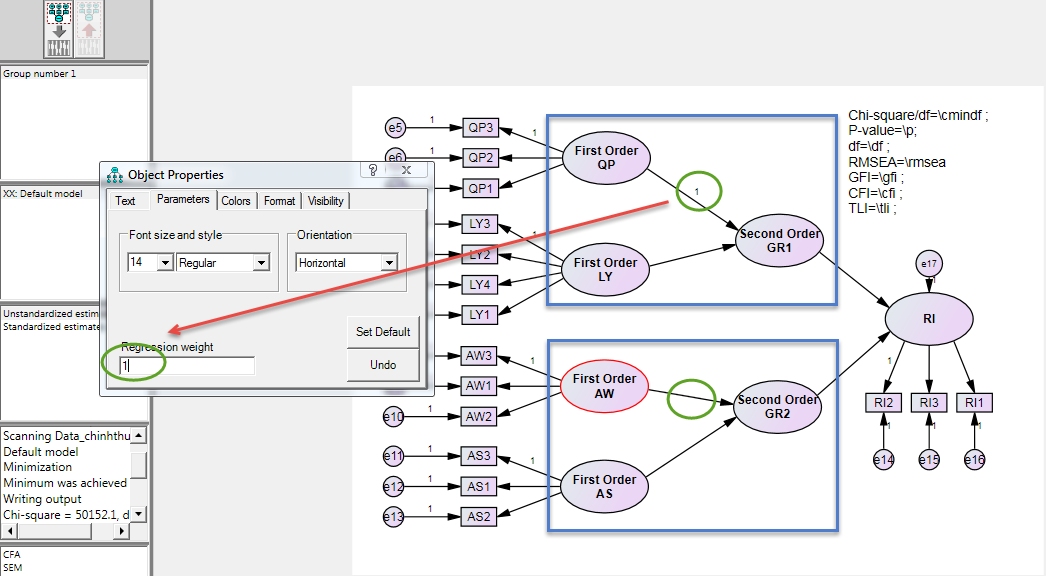
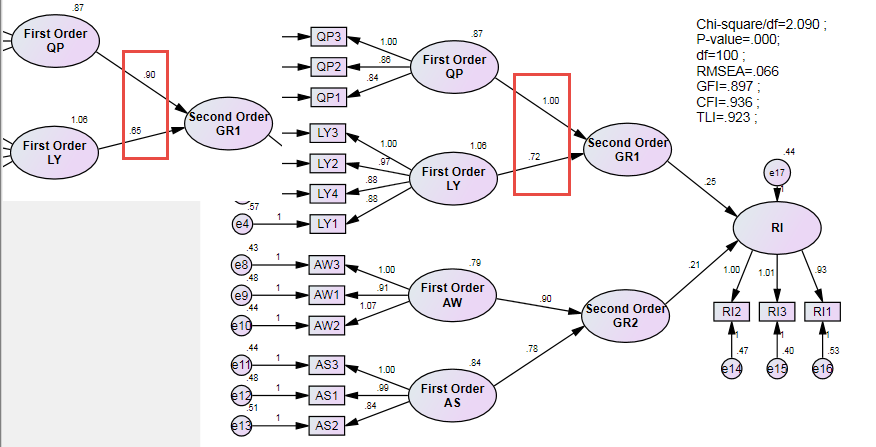
You can set any weight, if you set 1 then the weight of LY on GR1 is 0.72; but if you set 0.9 then the weight is now 0.65 (0.90*0.72/1.00 = 0.65). Or you can control both to be the same.
In STATA, the high-order structural model is similar to AMOS, however, you should not use STATA to run models with higher-order structure, because the algorithm in STATA is very complex, in addition it is too The Gauss iterative integration program is very time consuming, the results depend heavily on the number of iterations.
Below is an example running a higher order structural model using STATA.
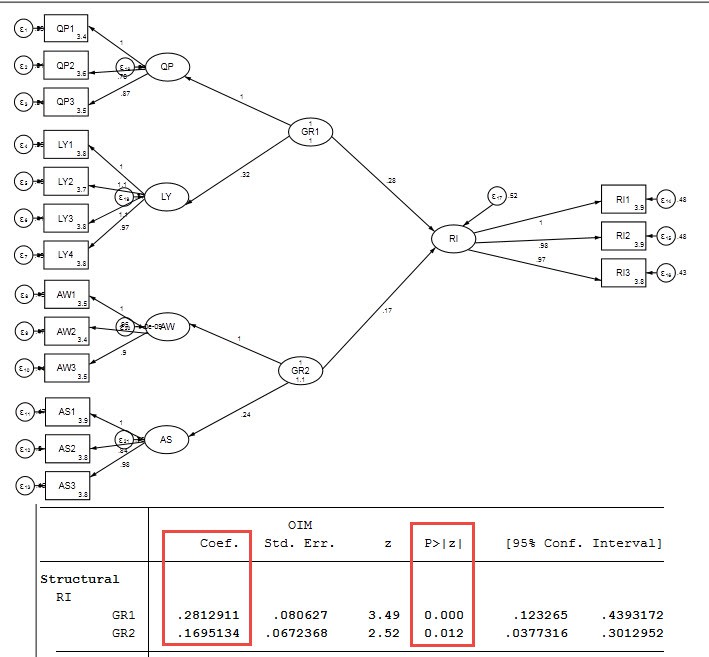
Some note:
Please quote the original text of Collier (2022) as follows:
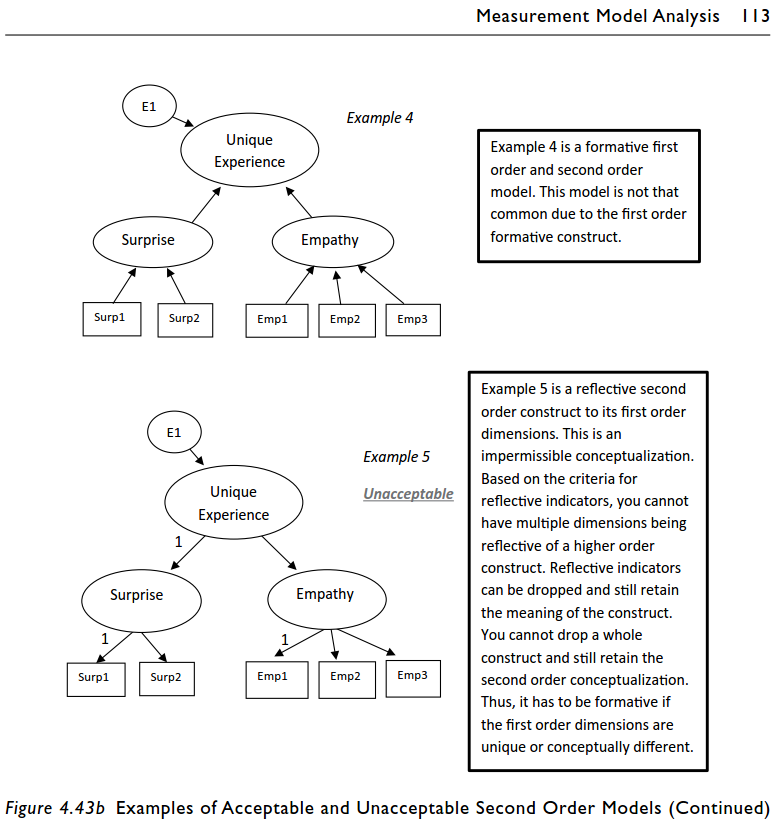
References
Collier, J. E. (2020). Applied structural equation modeling using AMOS: Basic to advanced techniques. Routledge.
Hair, J. F., Ringle, C. M., & Sarstedt, M. (2013). Partial least squares structural equation modeling: Rigorous applications, better results and higher acceptance. Long Range Planning, 46(1–2), 1–12.
Lohmöller, J.-B. (1989). Predictive vs. Structural modeling: Pls vs. ml. In Latent variable path modeling with partial least squares (pp. 199–226). Springer.
Wold, H. (1982). Models for knowledge. In The making of statisticians (pp. 189–212). Springer.






