R2 and Adjusted R2: Definitions, Meanings, and Differences
1. Definitions
1.1. R2 (Coefficient of Determination)
Definition: R2 represents the percentage of the total variance in the dependent variable (output variable) that is explained by the independent variables (input variables) in the model. The value of R2 ranges from 0 to 1 (or from 0% to 100%).
The formula for R2 is as follows:
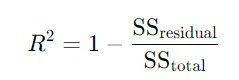
where SSresidualSS_{residual}SSresidual is the sum of squares of residuals, and SStotalSS_{total}SStotal is the total sum of squares.
Meaning: A higher R2 indicates that the model better explains the variability of the dependent variable. However, this measure does not take into account the number of independent variables in the model, which can lead to overestimating the model’s goodness-of-fit when more variables are added.
1.2. Adjusted R2
Definition: Adjusted R2 is a modified version of R2 that takes into account the number of independent variables and the sample size to prevent the model from becoming overly complex (overfitting) when more independent variables are added.
The formula for Adjusted R2 is as follows:
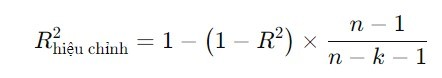
where:
- nnn is the number of observations (sample size),
- kkk is the number of independent variables.
Meaning: Adjusted R2 is usually lower than R2, especially as the number of independent variables increases. It only increases if the new independent variable actually adds meaningful explanatory power to the dependent variable.
2. Differences between R2 and Adjusted R2
Impact of Variables and Sample Size: Adjusted R2 takes into account the number of independent variables and the sample size, while R2 does not. Therefore, Adjusted R2 provides a more accurate assessment of the model’s goodness-of-fit, especially when comparing models with different numbers of independent variables.
Increase in Value: When additional independent variables are added to a model, R2 usually increases regardless of whether the new variable truly improves the model. In contrast, Adjusted R2 only increases if the new variable is genuinely useful.
In summary, when comparing models, especially those with different numbers of independent variables, Adjusted R2 is generally preferred because it offers a more realistic view of the model’s predictive capability.
3. References
Kutner, M. H., Nachtsheim, C. J., Neter, J., & Li, W. (2005). Applied Linear Statistical Models. McGraw-Hill.






