Understanding CB SEM and PLS SEM
Introduction to CB SEM and PLS SEM
CB-SEM (Covariance-Based Structural Equation Modeling):
CB-SEM is a data analysis method using covariance matrices to determine relationships between variables in a model. Widely used in social, business, and related fields, CB-SEM is a powerful statistical method allowing for the assessment of structural models of latent variables and their manifestations through path analysis and structural modeling.
CB-SEM requires data to be measured using regular methods and to follow a normal distribution. This method generates model evaluation indices such as homogeneity, reliability, and the impact of latent variables. CB-SEM utilizes structural models to test and determine relationships between variables in a complex network.
PLS-SEM (Partial Least Squares Structural Equation Modeling):
PLS-SEM is also a data analysis method used in social and business research. However, unlike CB-SEM, PLS-SEM does not require assumptions of normal distribution. Instead, PLS-SEM focuses on constructing structural models based on correlations between variables rather than correlations based on covariance.
PLS-SEM can be used in cases of small samples or when variables do not follow a normal distribution. It allows for the exploration of complex and multidimensional models and is often used in fields such as management, consumer behavior, marketing, and international business.
It is truly challenging to compare CB SEM and PLS SEM; it cannot be asserted that PLS SEM is a superior model to CB SEM. CB SEM and PLS SEM can be seen as complementary models rather than replacements. The strengths of CB SEM are the weaknesses of PLS SEM and vice versa. Depending on different research situations, researchers should consider using CB SEM or PLS SEM.
Difference between CB SEM and PLS SEM
The main difference between CB SEM and PLS SEM relates to their treatment of latent variables. According to Sarstedt et al. (2016), CB SEM divides the variance of each indicator into two parts: (i) common variance, shared by latent variables, and (ii) unique variance, including specific variance and shared variance from errors. Therefore, CB SEM assumes that the variance of indicators is perfectly explained by an unobservable variable or latent variable and random errors of each indicator. Thus, CB SEM pursues an approach called the “factor model.” Estimating this model is consistent with the philosophy of measurement model application (Sarstedt et al., 2016).
In contrast to CB SEM, PLS SEM does not divide variance into common variance and unique variance. The goal of PLS SEM is to explain the total variance of indicators instead of only explaining the correlation between indicators (Tenenhaus et al., 2005). In this case, PLS SEM considers latent variables represented by a composite variable, which is a linear combination of indicators. Thus, PLS SEM pursues a “composite model” to estimate measurement values for concepts.
Choosing between PLS SEM and CB SEM
Referencing Vũ Hữu Thành and Nguyễn Minh Hà (2023)
Choose PLS SEM when:
- The research goal is to identify input factors that impact output factors.
- Conducting predictive research.
- Conducting exploratory research or developing theory, especially studies aiming to extend relationships between concepts based on established theories.
- PLS SEM can support studies affirming relationships between concepts in situations where these relationships lack sufficient theoretical basis.
- The path model is complex (with many latent variables and indicators).
- Data have a small number of observations; PLS still performs well with large sample sizes.
- PLS SEM does not require assumptions about distribution. Whether the data follow a normal distribution or not is not an issue.
- Using latent variable values to conduct other analyses, especially higher-order models.
- The path model contains latent variables constructed by a formative measurement model.
- The study is conducted on secondary data, such as financial or accounting data, etc. In such studies, data types often lack measurement theories to form a measurement model, which is also a strength of the PLS SEM model.
Choose CB SEM when:
- The research goal is to test or confirm theory. This implies that the path model is built based on a theoretical framework developed beforehand. Two models need to be tested or confirmed: the measurement model and the structural model.
- The research goal is to compare theories to find a better alternative.
- The structural model has circular relationships, meaning variables have mutual relationships.
- The study requires an overall goodness-of-fit index.
- Large sample sizes and require normal or near-normal distribution.
- The measurement model of latent variables is best suited to the reflective measurement model.
Criteria for Evaluating CB SEM and PLS SEM Models
Since they are two different methods, the criteria for evaluating models are also different.
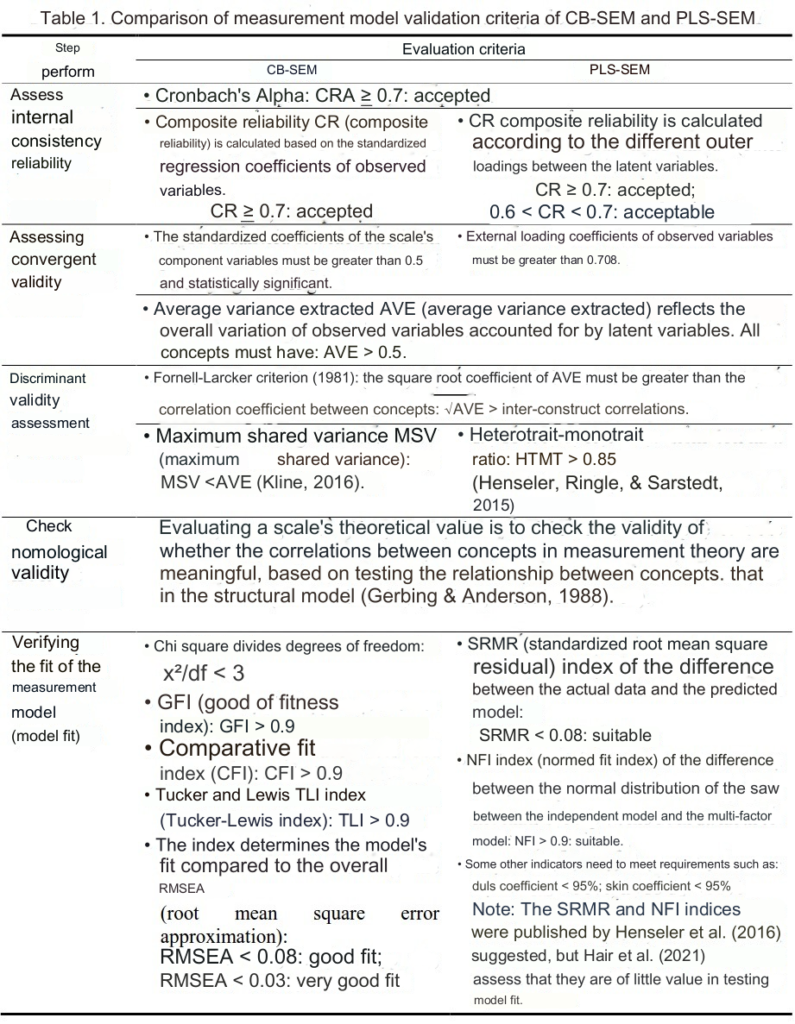
(Source: Trung and Nga (2022))
Additionally, in many cases, when GFI < 0.9, it’s because this index is very sensitive to the scale of the research sample; to achieve GFI > 0.9, the sample size for the study should be sufficiently large. In cases where GFI ≥ 0.8, the model’s adequacy is still acceptable (Baumgartner & Homburg, 1996).
References
Anderson, J. C., & Gerbing, D. W. (1988). Structural equation modeling in practice: A review and recommended two-step approach. Psychological Bulletin, 103(3), 411.
Baumgartner, H., & Homburg, C. (1996). Applications of structural equation modeling in marketing and consumer research: A review. International Journal of Research in Marketing, 13(2), 139–161.
Fornell, C., & Larcker, D. F. (1981). Structural equation models with unobservable variables and measurement error: Algebra and statistics. Journal of Marketing Research, 382–388.
Hair, J. F., Risher, J. J., Sarstedt, M., & Ringle, C. M. (2019). When to use and how to report the results of PLS-SEM. European Business Review, 31(1), 2–24.
Hair Jr, J. F., Hult, G. T. M., Ringle, C. M., Sarstedt, M., Danks, N. P., & Ray, S. (2021). Partial least squares structural equation modeling (PLS-SEM) using R: A workbook. Springer Nature.
Henseler, J., Hubona, G., & Ray, P. A. (2016). Using PLS path modeling in new technology research: updated guidelines. Industrial Management & Data Systems.
Henseler, J., Ringle, C. M., & Sarstedt, M. (2015). A new criterion for assessing discriminant validity in variance-based structural equation modeling. Journal of the Academy of Marketing Science, 43(1), 115–135.
Kline, R. B. (2016). Principles and practice of structural equation modeling. Guilford publications.
Sarstedt, M., Hair, J. F., Ringle, C. M., Thiele, K. O., & Gudergan, S. P. (2016). Estimation issues with PLS and CBSEM: Where the bias lies! Journal of Business Research, 69(10), 3998–4010.
Tenenhaus, M., Vinzi, V. E., Chatelin, Y.-M., & Lauro, C. (2005). PLS path modeling. Computational Statistics & Data Analysis, 48(1), 159–205.
Trung, T. T., & Nga, N. T. (2022). A comparison of CB-SEM and PLS-SEM methods in testing the effectiveness of online teacher training forms. Journal of Science, 19(2), 213.
Vũ Hữu Thành, & Nguyễn Minh Hà. (2023). Textbook on data analysis applying PLS-SEM model (1st ed.). National University Publishing House, Ho Chi Minh City.






