MEASUREMENT MODEL vs STRUCTURAL MODEL
EVALUATION CRITERIA
Hello everyone! Please cite the source amosleminh.com when sharing or copying content from our website. Sincerely thank you very much!
In this article, we will learn about two concepts commonly used in SEM analysis, which are measurement models and structural models. So, what is a measurement model? and what is the structural model? Next, let’s find out what these two types of models are like.
SEM models include two types of models: structural models and measurement models. Each type of model is built by a separate theory. The structural model is built based on background theory, while the measurement model is built on auxiliary theory (Henseler & Schuberth (2020) cited by Vu Huu Thanh & Nguyen Minh Ha (2023)).
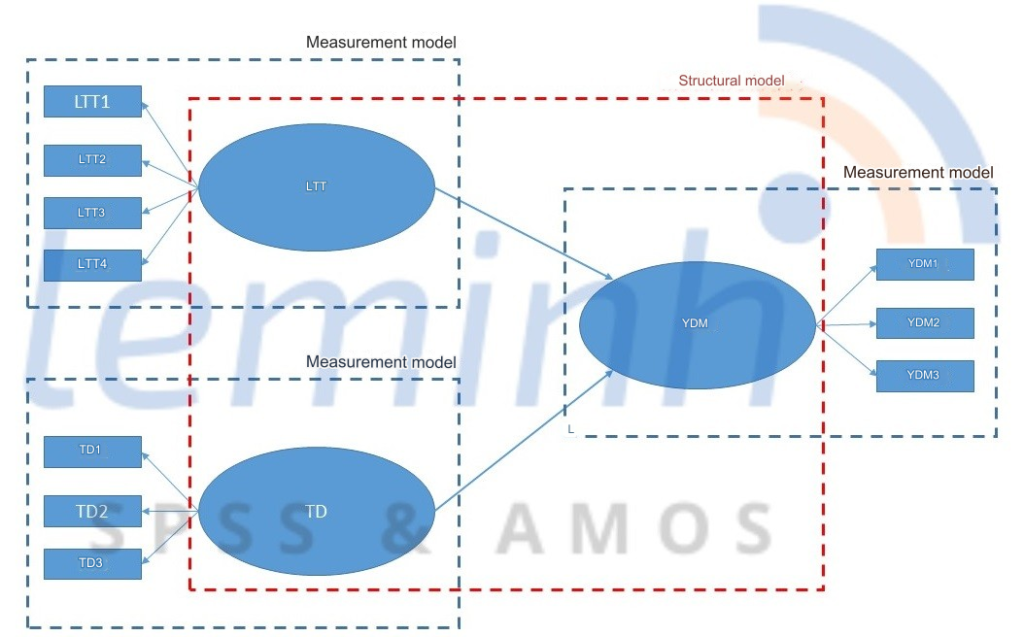
A. Measurement model (measurement model/outer model) is a model that shows the relationship between theoretical concepts (or structural variables)1 and indicators or observed variables. Thus, in the SEM model there will be many measurement models for different research concepts.
I. Evaluation of the measurement model
For CB SEM using AMOS, the main assessment of the measurement model is to evaluate the reliability, convergence and discrimination of the scale through the CFA method. We have presented the specific evaluation criteria of CFA many times in other shares. In this topic we will not discuss it again. You can refer to older topics for more information.
As for PLS SEM, the evaluation of the measurement model is divided into two types: (1) Evaluation of the reflective measurement model and (2) Evaluation of the constitutive measurement model.
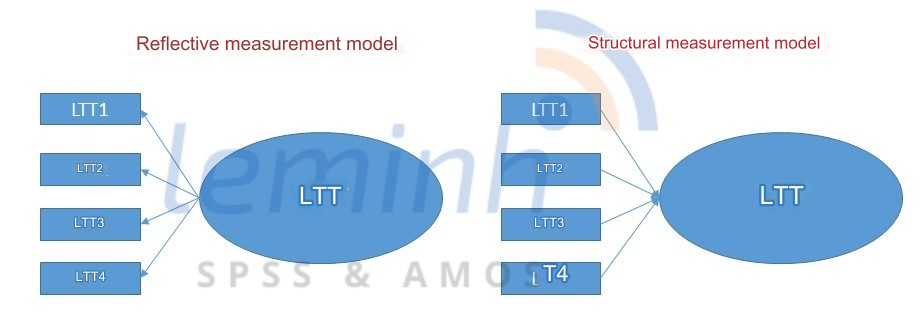
I.1. For the reflective measurement model, we need to evaluate the following 3 issues:
- Assess internal consistency reliability:
→ Outer loading factor ≥ 0.708. In some cases, the loading factor may be less than 0.708. In that case, we would eliminate that indicator, but we could also consider keeping it (Hulland (1999) cited by Vu Huu Thanh & Nguyen Minh Ha (2023)). According to Hair et al (2021), indicators with factor loadings between 0.4 and 0.7 should not be discarded. If removal increases the reliability of the scale, or does not affect content accuracy, remove the indicator.
→ Assess the level of internal consistency reliability through the composite reliability rating coefficient CR.
| CR > 0.9 | Some or all of the indicators may be measuring the same outcome from a latent variable (indicators that are very similar in meaning). You need to review the content accuracy and then remove the indicator and redo the analysis. |
| 0.6 ≤ CR ≤ 0.7 | Acceptable if used for exploratory research. If not find ways to improve CR and reanalyze the model PLS SEM. |
| CR < 0.6 | Unacceptable. It is necessary to consider rebuilding the measurement model or collecting more data and then re-analyzing the model. |
- Assess the level of convergence accuracy:
Evaluate the reliability of each indicator
| l ≥ 0.7 | The indicator reaches a reliable level |
| 0.4 ≤ l < 0.7 | Consider removing the indicator and re-analyzing the SEM model |
| l < 0.4 | Remove the indicator and perform the analysis again. |
l is the outer loading factor
Evaluate the degree of convergence accuracy
| AVE ≥ 0.5 | Achieve convergence precision |
| AVE < 0.5 | Does not reach the level of convergence accuracy. It is necessary to consider eliminating indicators or reconsidering ineffective measurement model building or data collection processes. |
Evaluate the level of discrimination accuracy:
| Compare the external loading factor and the diagonal loading factor (loading factor is on the diagonal) | The indicator of meeting the necessary condition is that the external loading factor is greater than the cross loading factor. In case the necessary conditions are not met, we need to consider removing the indicator or rebuilding the measurement model or reconsidering data collection. |
| HTMTij ≥ 0.9 | Accuracy in discrimination between pair of scales i and j is difficult to achieve. It is necessary to consider removing the indicator or rebuilding the measurement model or revisiting data collection. |
| HTMTij ≤ 0.85 | The scale achieves a level of discrimination accuracy. |
I.2. For the structural measurement model, we need to evaluate the following 3 issues:
This type of measurement model is quite rare in research. The testing standards for this type of model are also more complex. In principle, we will have 3 criteria to evaluate for this type of model. However, many scientific studies only mention two evaluation criteria: the assessment of the VIFs coefficient and the statistical significance of the Outer weights, without needing to evaluate the accuracy of the accuracy. converging. In this topic, we still mention the criteria for evaluating the accuracy of convergence so that you can grasp the preliminary technique.
- Assess the level of convergence accuracy:
For formative measurement models, assessing convergence accuracy is quite complicated, because according to Hair et al. (2021), we need to create a single-indicator model ( Single-item model). To make it easier to imagine, starting from here, we will consider evaluating a real model as follows:
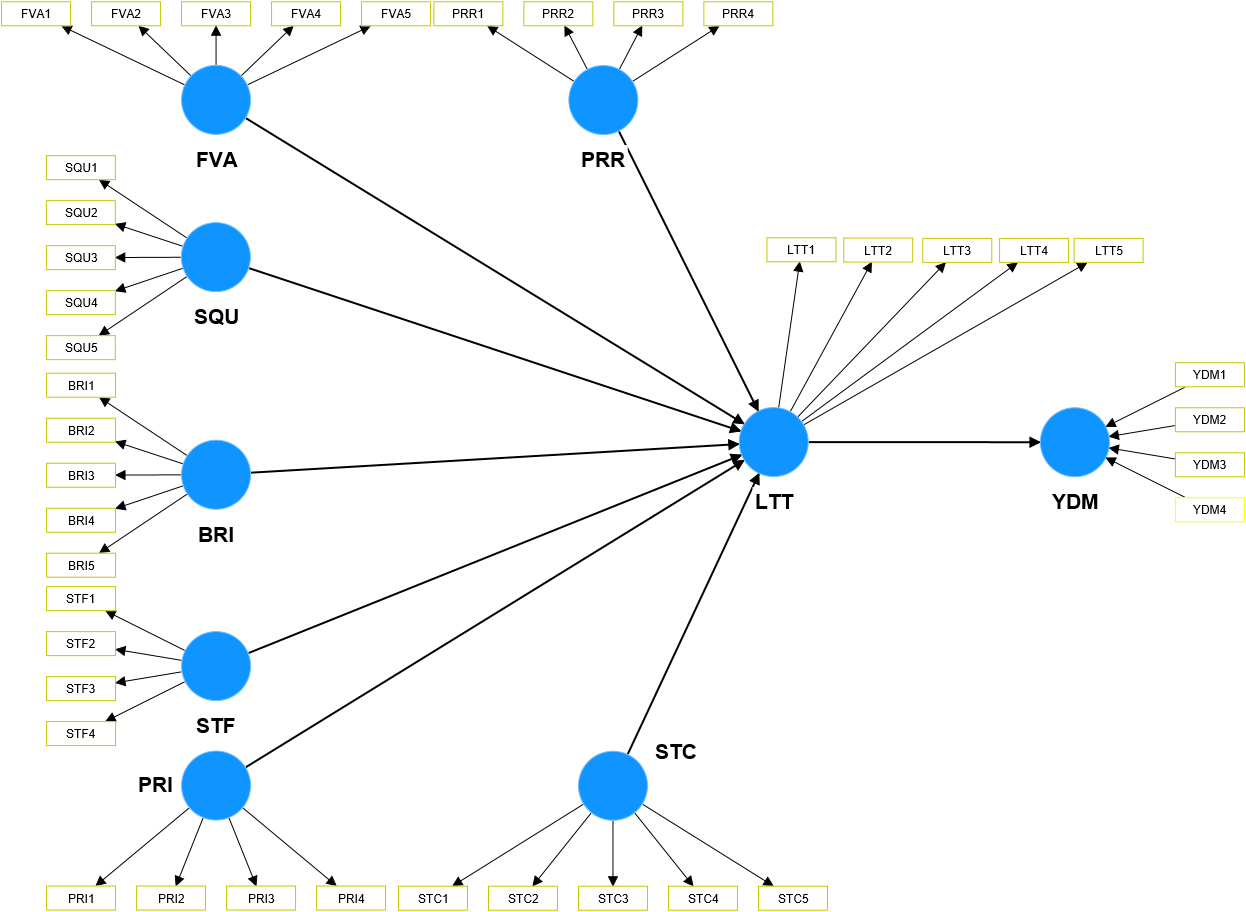
For this model, we see that there is only one concept, YDM, that is measured in a formative manner. Therefore, evaluating the measurement model requires evaluating the structural measurement model first, and then evaluating the reflective measurement model (we have presented the evaluation of the reflective measurement model in the following section). above).
As a first step, we need to create a single-indicator model to evaluate the measurement model for YDM.
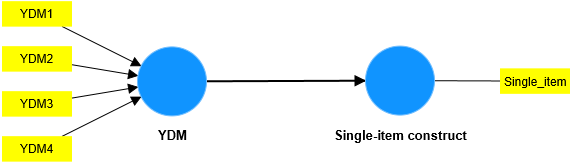
Checking that the regression value of the path is greater than or equal to 0.7 (and the P value is statistically significant) or R² ≥ 0.5 then it is concluded that the construct measurement model ensures convergence accuracy. The results of analyzing real situations show that the YDM measurement model ensures convergence accuracy.
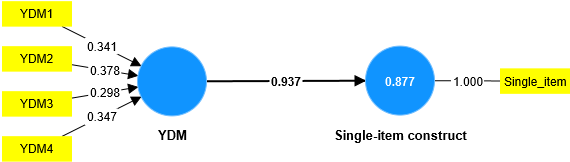
Our most complex and difficult problem in this rubric is the technique of creating the Single-item construct variable as we see above. Although Hair and colleagues (2021) mentioned it, it only stopped at the method introduction level. Instead, the author introduces the 3-step method of Cheah et al. (2018), detailed as follows (we would like to present the original text excerpted at EXHIBIT 5.3 page 144 of the book A primer on partial least squares structural equation modeling (PLS-SEM)):
 Cheah et al. (2018) have proposed the following three-step procedure for generating and validating global single items to be used as criterion variables in a redundancy analysis. Their procedure requires empirical data to be collected as part of a pilot study to validate the single item.
Cheah et al. (2018) have proposed the following three-step procedure for generating and validating global single items to be used as criterion variables in a redundancy analysis. Their procedure requires empirical data to be collected as part of a pilot study to validate the single item.
Step 1: Item generation
To generate a suitable single item, researchers need to carefully choose a theoretical definition of the concept of interest and identify popular measurement scales that build on this definition. Taking the scale items as input, researchers then need to create a measure that taps the most relevant aspect of the concept and the scale items. The resulting item should be checked for face validity by a panel of experts and members representing the target population.
Step 2: Reliability assessment
To assess the single item’s reliability, researchers can draw on the following formula:
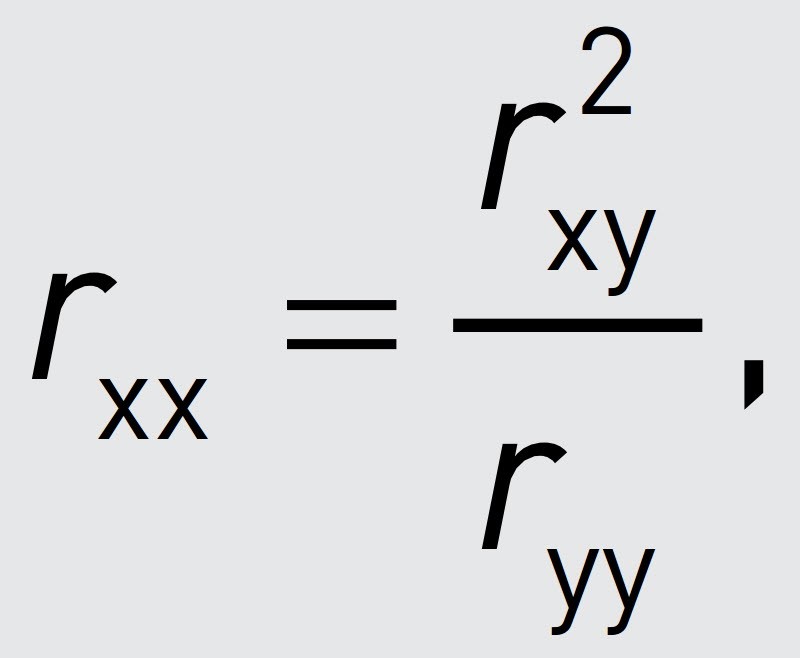
where rxx is the reliability estimate of the single-item measure x, ryy is the reliability of the reflective multi-item measure of the same concept (e.g., as depicted by ρA; Chapter 4), and rxy is the correlation between the single-item and multi-item measure of the same concept. Hence, reliability assessment by means of this formula requires the simultaneous administration of a single-item and a multi-item measure of the same concept, for example, as part of a pilot study. The internal consistency reliability should be 0.7 or higher.
Step 3: Convergent and criterion validity assessment
Assessing the single item’s convergent validity requires correlating the single item with the alternative reflective multi-item measure from Step 2. This correlation should be 0.7 or higher. To assess the item’s criterion validity, researchers need to correlate it with a criterion measure with which it is supposed to be related. Defining a firm threshold for an acceptable degree of criterion validity is difficult, as this depends on the constructs under consideration. However, at a bare minimum, the correlation should be significant.

The Single-item variable is created by building a general scale with a single question (item), for example, Purchase intention is built with a question like: In general, I want to buy the product/service. this case? Note that the scale of the Single-item variable and the YDM scale must have the same form and similar size (for example, if you use a 5-point likert to measure YDM, the Single-item must also use a 5-point likert). ).
In general, creating a Single-item variable in this case is not simple, because if the general question is not carefully researched, it will create misleading results, thereby affecting the testing problem. The scale. Because of the difficulty, complexity and cost of creating Single-item variables, scientific research currently often ignores this evaluation criterion for formative models. These are instructional videos from data experts around the world. You can refer to them here: video 1; video 2; v.v.
♥ Note that, when coming to Le Minh Data Service, when you need to evaluate this criterion, we are ready to support and guide you in detail on how to create single items to ensure ensure the criteria for evaluating the accuracy of convergence meet the requirements.
- Assess the level of multicollinearity:
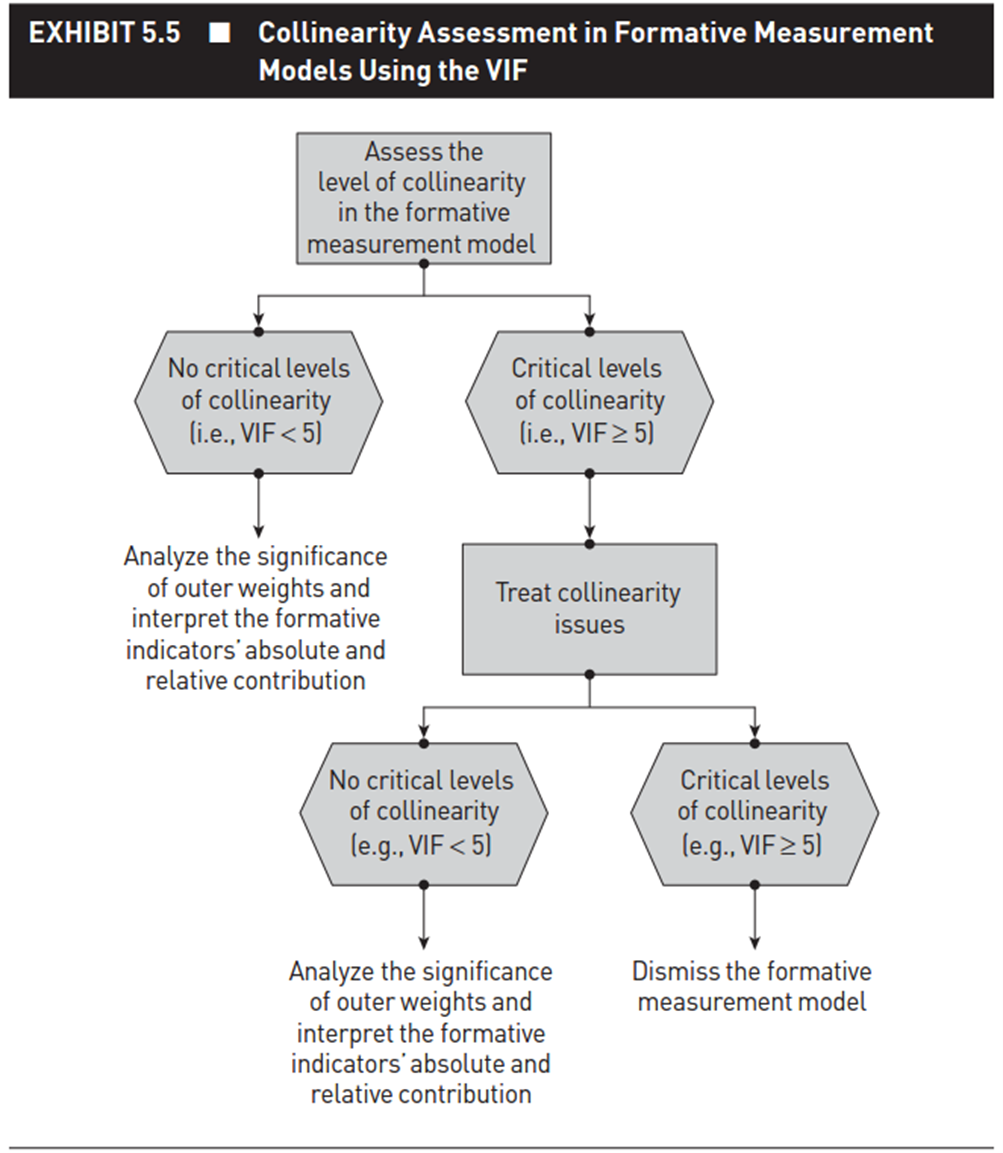
The assessment of the degree of multicollinearity of the construct measurement model needs to be considered on the established single-indicator model. According to Hair et al. (2021), if VIF < 5, it is concluded that the indicators do not experience multicollinearity. In some cases where VIF ≥ 5, we need to consider removing indicators with VIF ≥ 5. Note that, due to the theoretical characteristics of the formative model, removing indicators is not recommended because will affect construct quality. You should review the entire model building process and survey implementation process to ensure the standardization of input data.

The results of analyzing the practical model show that the indicators ensure multicollinearity.
Diagram representing the VIF testing process for the formative model (source: Hair et al. (2021)):
- Evaluate the statistical significance of the external weight value (using the bootstrap method):
Note, this evaluation step we will perform on the main model. Run bootstrap (with a recommended N of 5000). We evaluate the Pvalue of the external weights. If P value is less than 5%, it is concluded that the weight is statistically different from zero and the structural measurement model meets the requirements.
In many cases, if the P value of the outer weights does not reach statistical significance (>5%), we should not rush to eliminate the variable, we need to continue to evaluate the statistical significance of the outer loading coefficient. of indicators in the formative model. If the external loading coefficient of the indicators of the formative model is ≥ 5, the indicators are still retained in the model even though they are not meaningful. In case the external load factor is < 5, it is necessary to further evaluate its statistical significance. If the level of statistical significance meets the requirements, consider whether to remove that indicator from the formative model (note that this removal needs to be carefully considered because of the nature of the formative model), if The statistical significance level does not meet the requirements, then remove that variable from the formative model. The following is a flow chart for checking the outer weights coefficient cited from Hair et al. (2021).
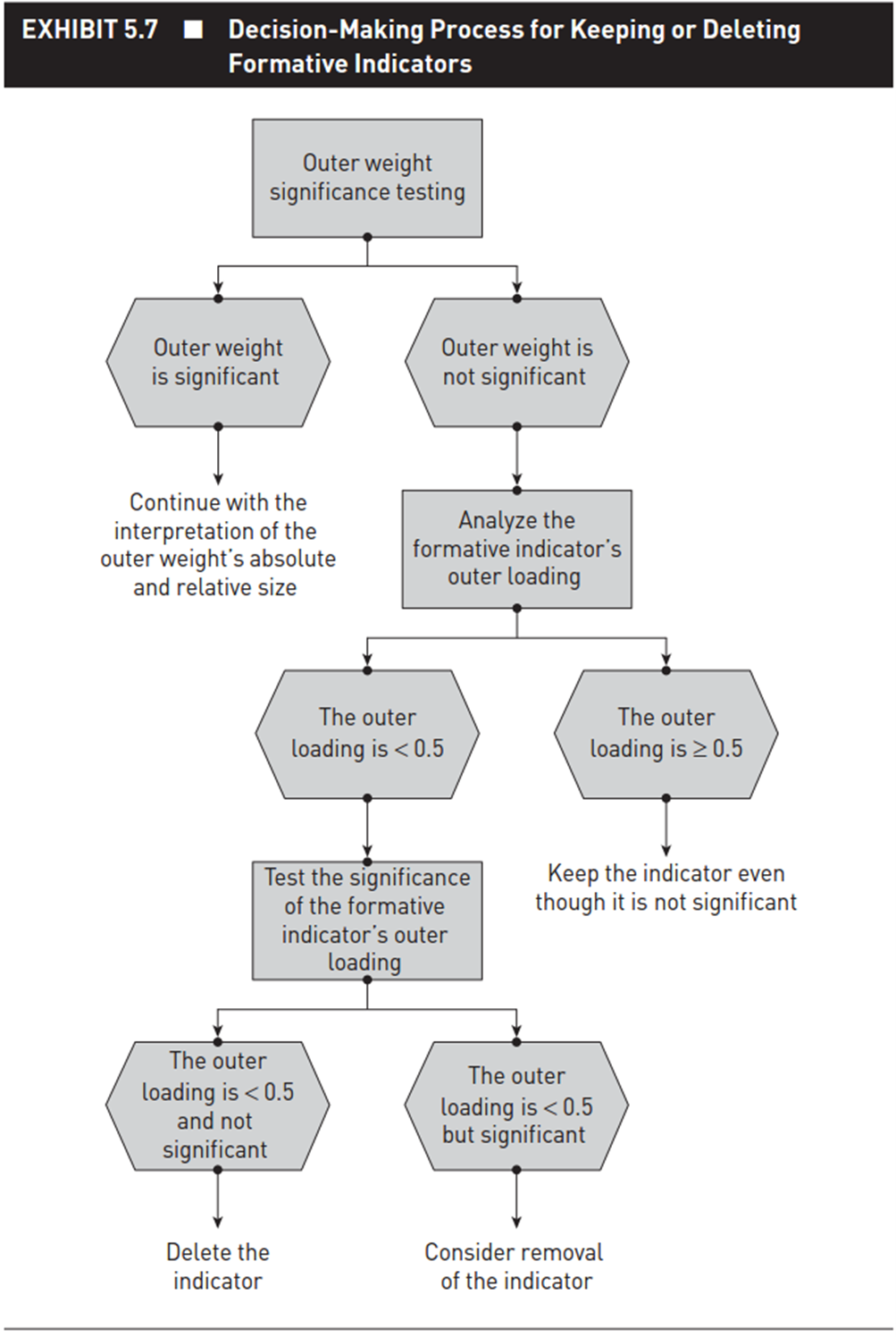
So, here we have finished evaluating the measurement model. Next, we will look at evaluating the structural model.
B. Structural model (structural model/ inner model) is a model that shows the relationships between research concepts in the SEM model. Thus, a SEM model has only one structural model. Evaluation of the SEM structural model, here, we divide into two types: one is the CB SEM model, the other is the PLS SEM model.
I.1. For the CB SEM model, running the model with AMOS is very familiar to us. To evaluate the CB SEM structural model, you carry out the procedure to evaluate the SEM model running AMOS as we have presented in older topics.
I.2. For the PLS SEM model, the evaluation of the structural model is performed as follows:
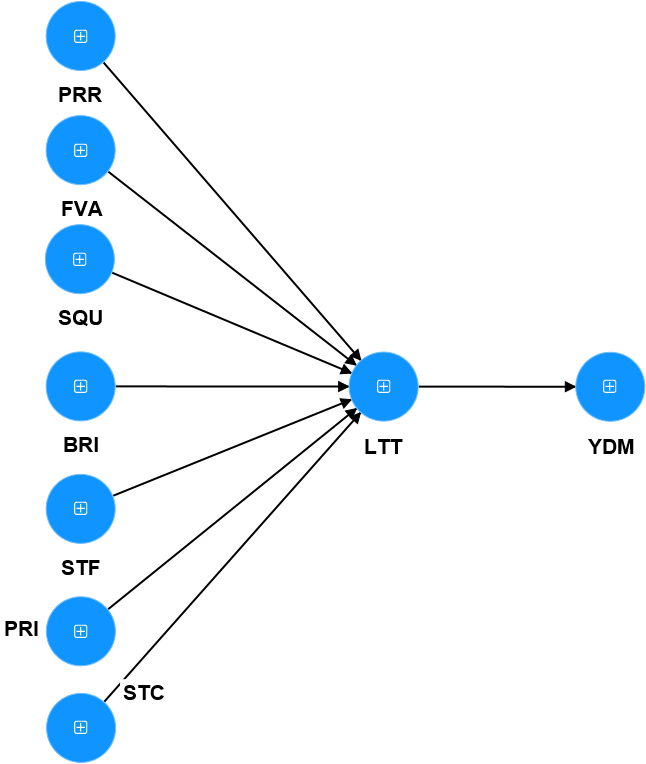
- Assess the degree of multicollinearity among explanatory variables in a SEM model. Note, we consider VIF in the Inner model section in the PLS SEM algorithm from SmartPLS. If VIF ≤ 5, it is concluded that multicollinearity does not appear. If at this point, VIF > 5, then the only way is to reconsider the entire input theory and re-examine the data.
- Evaluate statistical significance and conclude research hypotheses.
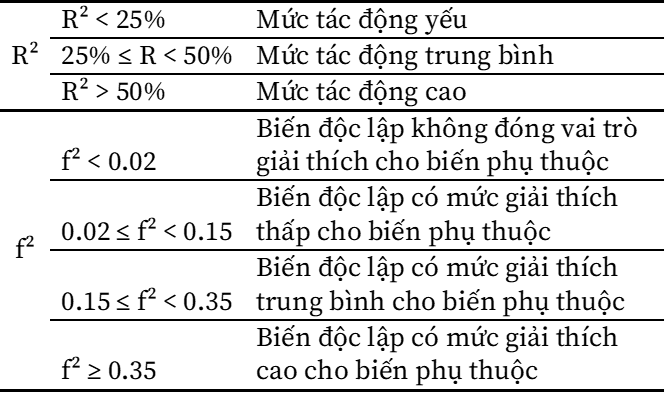
- Evaluate the explanatory role of the first variable to the dependent variable through the coefficient R², adjusted R², and f² index. For detailed reviews, you can refer to our older topics.
Assess the level of forecasting accuracy through the Q² coefficients and evaluate the forecasting effectiveness of an explanatory variable through the IP analysis chart, using the IPMA method (we have presented it in detail in in an older topic).
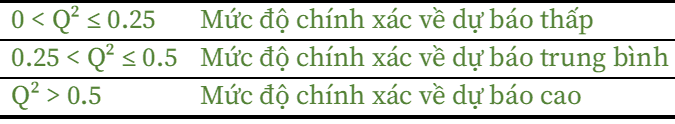
At this point, we have finished evaluating the structural model. Thus, when testing the PLS SEM model, we will evaluate both the measurement model and the structural model.

- Readers need to distinguish between theoretical concepts and structural variables. Theoretical concepts are measured by one of three types of structural variables. According to (Vu Huu Thanh & Nguyen Minh Ha, 2023), structural variables have 3 types: reflective latent variable, causal latent variable, and emergent variable. To learn more deeply, there are currently many textbooks written in detail about this, we would like to introduce to readers the textbook Data Analysis applying the PLS SEM model (advanced part) by Vu Huu Thanh & Nguyen Minh Ha (2023).
References
Hair Jr, J. F., Hult, G. T. M., Ringle, C. M., & Sarstedt, M. (2021). A primer on partial least squares structural equation modeling (PLS-SEM). Sage publications.
Henseler, J., & Schuberth, F. (2020). Using confirmatory composite analysis to assess emergent variables in business research. Journal of Business Research, 120, 147–156.
Hulland, J. (1999). Use of partial least squares (PLS) in strategic management research: A review of four recent studies. Strategic Management Journal, 20(2), 195–204.
Vu Huu Thanh, & Nguyen Minh Ha. (2023). Data analysis textbook applying the PLS – SEM model (1st ed.). Ho Chi Minh City National University Publishing House.
Sarstedt, M., Hair Jr, J. F., Cheah, J. H., Becker, J. M., & Ringle, C. M. (2019). How to specify, estimate, and validate higher-order constructs in PLS-SEM. Australasian marketing journal, 27(3), 197-211.






